The 5 Most Popular Regression Techniques

Regression is a widely used method for modeling relationships among variables. Different regression techniques can suit various datasets depending on the problem. This article highlights the 5 most popular regression techniques and the types of datasets wherein these are most effective.

Introduction

Although, we won’t go into the details of the assumptions for each technique in this article, but it’s important to understand them before you apply any method. While not every assumption will apply in every situation, they can give you a good sense of how reliable the model’s relationships are and how well it might predict future outcomes.

Ordinary Linear Regression
Polynomial Regression
Stepwise regression
Ridge regression
Lasso Regression

Handling Overfitting in Machine Learning

Overfitting is one of the key challenges in Machine Learning. This occurs when model performance on training data is…

indiequant.medium.com

Ordinary Linear Regression (OLS)

Assumptions

Below is a quick summary on assumptions:

Linearity: The relationship between X and the mean of Y is linear.
Homoscedasticity: The variance of residual is the same for any value of X.
Independence: Observations are independent of each other.
Normality: For any fixed value of X, Y is normally distributed.

Details:

Regression analysis is commonly used for modeling the relationship between a single dependent variable Y and one or more predictors. When we have one predictor, we call this “simple” linear regression:

E[Y] = β0 + β1X

That is, the expected value of Y is a straight-line function of X. The betas are selected by choosing the line that minimizing the squared distance between each Y value and the line of best fit. The betas are chosen such that they minimize this expression:

∑ (yi — (β0 + β1Xi))^2

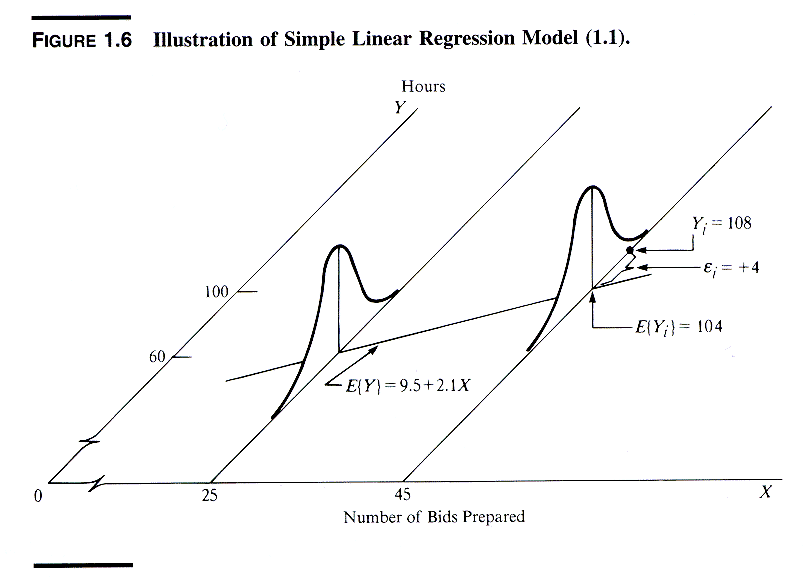
Source: https://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/R/R5_Correlation-Regression/R5_Correlation-Regression4.html

Implementation example

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Step 1: Create dummy data
np.random.seed(0)  # Set seed for reproducibility
X = 2 * np.random.rand(100, 1)  # Generate 100 random samples for the feature (between 0 and 2)
y = 4 + 3 * X + np.random.randn(100, 1)  # Create target variable with a linear relationship plus some noise

# Step 2: Convert to DataFrame for better visualization (optional)
data = pd.DataFrame(np.hstack((X, y)), columns=['Feature', 'Target'])

# Step 3: Split the data into training and testing sets
# We will use 80% of the data for training and 20% for testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 4: Create and fit the linear regression model
model = LinearRegression()  # Instantiate the model
model.fit(X_train, y_train)  # Fit the model to the training data

# Step 5: Make predictions using the test set
y_pred = model.predict(X_test)  # Use the model to predict values for the test set

# Step 6: Evaluate the model's performance
mse = mean_squared_error(y_test, y_pred)  # Calculate Mean Squared Error
r2 = r2_score(y_test, y_pred)  # Calculate R^2 score

# Step 7: Output the model's parameters and evaluation metrics
print("Coefficients:", model.coef_)  # Print the coefficients of the model
print("Intercept:", model.intercept_)  # Print the intercept of the model
print("Mean Squared Error:", mse)  # Print the Mean Squared Error
print("R^2 Score:", r2)  # Print the R^2 score

# Step 8: Visualize the results
plt.scatter(X_test, y_test, color='blue', label='Actual')  # Plot actual values
plt.scatter(X_test, y_pred, color='red', label='Predicted')  # Plot predicted values
plt.plot(X_test, y_pred, color='green', linewidth=2, label='Regression Line')  # Plot the regression line
plt.xlabel('Feature')  # Label for the x-axis
plt.ylabel('Target')  # Label for the y-axis
plt.title('OLS Regression Example')  # Title of the plot
plt.legend()  # Show the legend
plt.show()  # Display the plot

Sentiment Analysis using Deep Learning (BERT)

Sentiment analysis is one of the classic machine learning problems which finds use cases across industries. For…

indiequant.medium.com

Polynomial Regression

Assumptions

For polynomial regression models we assume that:

The relationship between the dependent variable y and any independent variable xi is linear or curvilinear (specifically polynomial),

2. The independent variables xi are independent of each other

3. The errors are independent, normally distributed with mean zero and a constant variance (OLS).

Clearly there is significant overlap with the assumptions of OLS mentioned above.

Details

Understanding Polynomial Regression

Polynomial Representation

A polynomial can be expressed as:

y = b0 + b1 * x + b2 * x**2 + b3 * x**3 + bn * x**n

In this formula, the exponents of the variable x are constants.

Example Visualization:

Below, you can see an animation of a parabola approximating the flight path of a ball which depicts the polynomial relationship.

Understanding Polynomial Models

Polynomial models can be described in two ways:

a. They are linear with respect to the coefficients bi ince these parameters have an exponent of 1.
b. They are non-linear with respect to the variables due to terms like x**2, x**3 etc.

Generating Polynomial Terms

Polynomial terms are created by raising the variable values to a specific power. however it does come with multicollinearity implications:

y = b0 + b1 * x + b2 * x**2

In this equation, the variable \( x \) appears twice:

- Once as b1*x
- Once as b2*(x**2)

Since x and x**2 are related, this can lead to multicollinearity issues, which can affect the model’s reliability.

Implementation example

# Import necessary libraries
import numpy as np                  # For numerical operations
import matplotlib.pyplot as plt     # For plotting
from sklearn.model_selection import train_test_split  # For splitting the dataset
from sklearn.preprocessing import PolynomialFeatures   # For generating polynomial features
from sklearn.linear_model import LinearRegression      # For performing linear regression
from sklearn.metrics import mean_squared_error, r2_score  # For evaluating the model

# Step 1: Generate some dummy data using a polynomial function
np.random.seed(0)  # Set seed for reproducibility
X = 2 * np.random.rand(100, 1)  # Generate 100 random samples for the feature (X between 0 and 2)

# Create target variable (y) using a polynomial function, e.g., y = 1 - 2x + 3x^2 + noise
y = 1 - 2 * X + 3 * X**2 + np.random.randn(100, 1)  # Adding some noise

# Step 2: Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 3: Transform the features into polynomial features
degree = 2  # Specify the degree of the polynomial
poly_features = PolynomialFeatures(degree=degree)  # Create a PolynomialFeatures object
X_poly_train = poly_features.fit_transform(X_train)  # Transform the training data
X_poly_test = poly_features.transform(X_test)  # Transform the test data

# Step 4: Create and fit the linear regression model
model = LinearRegression()  # Instantiate the model
model.fit(X_poly_train, y_train)  # Fit the model to the transformed training data

# Step 5: Make predictions using the test set
y_pred = model.predict(X_poly_test)  # Predict values for the test set

# Step 6: Evaluate the model's performance
mse = mean_squared_error(y_test, y_pred)  # Calculate Mean Squared Error
r2 = r2_score(y_test, y_pred)  # Calculate R^2 score

# Step 7: Output the model's parameters and evaluation metrics
print("Coefficients:", model.coef_)  # Print the coefficients of the model
print("Intercept:", model.intercept_)  # Print the intercept of the model
print("Mean Squared Error:", mse)  # Print the Mean Squared Error
print("R^2 Score:", r2)  # Print the R^2 score

# Step 8: Visualize the results
plt.scatter(X_test, y_test, color='blue', label='Actual')  # Plot actual values as blue dots
plt.scatter(X_test, y_pred, color='red', label='Predicted')  # Plot predicted values as red dots
# Plot the polynomial regression curve
X_range = np.linspace(0, 2, 100).reshape(-1, 1)  # Create a range of X values for plotting
X_range_poly = poly_features.transform(X_range)  # Transform this range to polynomial features
y_range_pred = model.predict(X_range_poly)  # Predict the corresponding y values
plt.plot(X_range, y_range_pred, color='green', linewidth=2, label='Polynomial Regression Line')  # Plot the regression line
plt.xlabel('Feature (X)')  # Label for the x-axis
plt.ylabel('Target (y)')  # Label for the y-axis
plt.title('Polynomial Regression Example with Polynomial Target')  # Title of the plot
plt.legend()  # Show the legend
plt.grid()  # Add a grid for better readability
plt.show()  # Display the plot

How I Created Animated Choropleth Map and Bar Chart Race using Python

We will use animated Python visualisations to observe trends of state-wise forest cover over the years in India

python.plainenglish.io

Stepwise Regression

This section covers stepwise regression, a method where we build our regression model by gradually adding and removing predictor variables until no more changes make sense. The aim is to create a useful model without any variables which do not improve relationship modeling. However, if we don’t include all the relevant variables that affect the response, we risk ending up with a model that misses important insights and is misleading. So, it’s essential to ensure our list of candidate predictors includes everything that truly influences the outcome.

Assumptions and Limitations

The same assumptions and qualifications apply here as applied to OLS. Note that outliers can have a large impact on these stepping procedures, so you must make some attempt to remove outliers from consideration before applying these methods to your data.

The greatest limitation with these procedures is one of sample size. A good rule of thumb is that you have at least five observations for each variable in the candidate pool. If you have 50 variables, you should have 250 observations. With less data per variable, these search procedures may fit the randomness that is inherent in most datasets and spurious models will be obtained.

Details

Below are the steps followed

Initialize: Start with an empty model and define a significance level (e.g., α = 0.05).

2. Candidate Selection: Identify all candidate predictor variables.

3. Iterate Until Convergence:

Adding Step:

For each candidate not in the model, fit the model with that predictor and check the p-value.
Add the predictor with the smallest p-value if it’s less than the significance level.

Removing Step:

For each predictor in the model, fit the model without it and check the p-value.
Remove the predictor with the largest p-value if it exceeds the significance level.

4. Final Model:

Stop when no predictors are added or removed. The resulting model includes only significant predictors.

Implementation example

# Import necessary libraries
import numpy as np                  # For numerical operations
import pandas as pd                 # For data manipulation
import matplotlib.pyplot as plt     # For plotting
from sklearn.model_selection import train_test_split  # For splitting the dataset
from sklearn.linear_model import LinearRegression      # For performing linear regression
from sklearn.metrics import mean_squared_error, r2_score  # For evaluating the model
import statsmodels.api as sm        # For statistical modeling

# Step 1: Generate dummy data
np.random.seed(0)  # Set seed for reproducibility

# Create 10 predictor variables
X1 = np.random.rand(100)
X2 = np.random.rand(100) * 0.1  
X3 = np.random.rand(100) * .2 + .5 
X4 = - 0.5 * X3 + np.random.rand(100) * 0.1  # X4 is correlated with X1 and X3
X5 = np.random.rand(100)
X6 = -X2 + np.random.rand(100) * 0.1  # X6 is correlated with X2
X7 = np.random.rand(100)
X8 = 3 * X7 + np.random.rand(100) * 0.1  # X8 is correlated with X7
X9 = np.random.rand(100)
X10 = 0.3 * X3 + 0.7 * X4 + np.random.rand(100) * 0.1  # X10 is correlated with X3 and X4

# Combine into a DataFrame
X = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3, 'X4': X4,
                  'X5': X5, 'X6': X6, 'X7': X7, 'X8': X8,
                  'X9': X9, 'X10': X10})
y = 3 + 2 * X1 - X2 + 0.5 * X3 + np.random.rand(100) * 0.5  # Response variable

# Step 2: Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 3: Perform Stepwise Selection
def stepwise_selection(X, y, threshold_in=0.05, threshold_out=0.05):
    """
    Perform stepwise selection using forward selection and backward elimination.
    
    :param X: DataFrame of predictor variables
    :param y: Target variable
    :param threshold_in: Significance level for adding predictors
    :param threshold_out: Significance level for removing predictors
    :return: Selected features
    """
    initial_features = X.columns.tolist()  # List of initial features
    selected_features = []  # List of selected features

    # Forward Selection
    while True:
        changed = False
        # Calculate p-values for each feature
        pvals = []
        for feature in initial_features:
            model = sm.OLS(y, sm.add_constant(X[selected_features + [feature]])).fit()  # Fit model
            pvals.append((feature, model.pvalues[feature]))  # Store feature and its p-value
        
        # Sort by p-value
        pvals.sort(key=lambda x: x[1])
        
        # Check if the lowest p-value is below the threshold
        if pvals[0][1] < threshold_in:
            selected_features.append(pvals[0][0])  # Add feature to selected features
            initial_features.remove(pvals[0][0])  # Remove it from initial features
            changed = True  # A feature was added
        if not changed:
            break  # Exit if no features were added

    # Backward Elimination
    while True:
        changed = False
        # Calculate p-values for selected features
        model = sm.OLS(y, sm.add_constant(X[selected_features])).fit()  # Fit model
        pvals = model.pvalues[1:]  # Get p-values (skip intercept)
        
        # Check if the highest p-value is above the threshold
        if (pvals > threshold_out).any():
            worst_feature = pvals.idxmax()  # Find the feature with the highest p-value
            selected_features.remove(worst_feature)  # Remove it from selected features
            changed = True  # A feature was removed
        if not changed:
            break  # Exit if no features were removed

    return selected_features

# Run stepwise selection
selected_features = stepwise_selection(X_train, y_train)
print("Selected features:", selected_features)

# Step 4: Fit the final model with selected features
final_model = sm.OLS(y_train, sm.add_constant(X_train[selected_features])).fit()
print(final_model.summary())

# Step 5: Make predictions using the test set
y_pred = final_model.predict(sm.add_constant(X_test[selected_features]))

# Step 6: Evaluate the model's performance
mse = mean_squared_error(y_test, y_pred)  # Calculate Mean Squared Error
r2 = r2_score(y_test, y_pred)  # Calculate R^2 score

# Output evaluation metrics
print("Mean Squared Error:", mse)  # Print MSE
print("R^2 Score:", r2)  # Print R^2 score

# Step 7: Visualize the actual vs predicted values
plt.scatter(y_test, y_pred, color='blue')  # Plot actual values vs predicted values
plt.plot([y.min(), y.max()], [y.min(), y.max()], color='red', linewidth=2)  # Line of equality
plt.xlabel('Actual values')  # Label for x-axis
plt.ylabel('Predicted values')  # Label for y-axis
plt.title('Actual vs Predicted Values')  # Title of the plot
plt.grid()  # Add grid for better readability
plt.show()  # Display the plot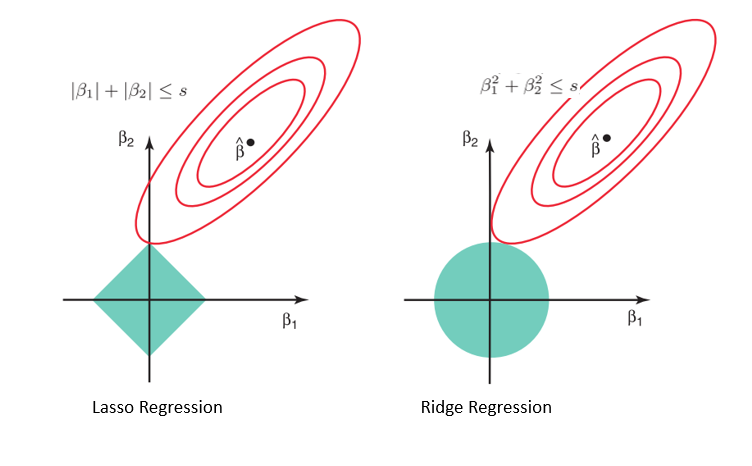

source: https://online.stat.psu.edu/stat508/

Introduction to BIRCH Clustering & Python Implementation

Introduction to Clustering & need for BIRCH

python.plainenglish.io

Ridge Regression

Ridge regression is a statistical technique used to estimate the coefficients of multiple regression models, particularly when the independent variables exhibit high multicollinearity.

Assumptions

The assumptions of ridge regression are the same as those of linear regression: linearity, constant variance, and independence. However, as ridge regression does not provide confidence limits, the distribution of errors to be normal need not be assumed.

Details

Multicollinearity Issues:

Causes high variances in coefficient estimates, leading to poor predictions, even though least squares remain unbiased.

Key Concepts:

L2 Regularization: Adds a penalty based on the square of the coefficients to the cost function.

Cost Function: Minimize ||Y−Xθ||**2 + λ*||θ||**2 whereY: Actual values; X: Independent variables; θ: Coefficients; λ: Penalty term.

First Term (Residual Sum squared): This part measures the difference between the actual values and the predicted values. It captures how well the model fits the training data.

Penalty Term: This term penalizes large coefficients by adding the sum of the squares of the coefficients to the cost function.

Role of λ:

Higher λ: Greater penalty and smaller coefficients; Lower λ: Lesser penalty, coefficients approach those from ordinary least squares.

Benefits

Coefficient Shrinkage: Reduces the impact of multicollinearity.
Simplified Model: Easier interpretation and improved predictive performance.

Implementation example

# Import necessary libraries
import numpy as np                  # For numerical operations
import pandas as pd                 # For data manipulation
import matplotlib.pyplot as plt     # For plotting
from sklearn.model_selection import train_test_split  # For splitting the dataset
from sklearn.linear_model import Ridge          # For ridge regression
from sklearn.metrics import mean_squared_error, r2_score  # For evaluating the model

# Step 1: Generate dummy data
np.random.seed(42)  # Set seed for reproducibility

# Create 10 predictor variables
X1 = np.random.rand(100)
X2 = np.random.rand(100) * 0.1  
X3 = np.random.rand(100) * .2 + .5 
X4 = 0.5 * X1 - 0.5 * X3 + np.random.rand(100) * 0.1  # X4 is correlated with X1 and X3
X5 = np.random.rand(100)
X6 = -X2 + np.random.rand(100) * 0.1  # X6 is correlated with X2
X7 = np.random.rand(100)
X8 = 3 * X7 + np.random.rand(100) * 0.1  # X8 is correlated with X7
X9 = np.random.rand(100)
X10 = 0.3 * X3 + 0.7 * X4 + np.random.rand(100) * 0.1  # X10 is correlated with X3 and X4

# Combine into a DataFrame
X = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3, 'X4': X4,
                  'X5': X5, 'X6': X6, 'X7': X7, 'X8': X8,
                  'X9': X9, 'X10': X10})
y = 3 + 2 * X1 - 1 * X2 + 0.5 * X3 + np.random.rand(100) * 0.5  # Response variable with noise

# Step 2: Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 3: Fit Ridge Regression Model
# Initialize Ridge regression with a specific alpha value
alpha_value = 1.0  # Regularization strength
ridge_model = Ridge(alpha=alpha_value)

# Fit the model to the training data
ridge_model.fit(X_train, y_train)

# Step 4: Make Predictions
y_pred = ridge_model.predict(X_test)  # Predict on the test set

# Step 5: Evaluate the Model
mse = mean_squared_error(y_test, y_pred)  # Calculate Mean Squared Error
r2 = r2_score(y_test, y_pred)  # Calculate R^2 score

# Output evaluation metrics
print("Mean Squared Error:", mse)  # Print MSE
print("R^2 Score:", r2)  # Print R^2 score

# Step 6: Visualize the Actual vs. Predicted Values
plt.scatter(y_test, y_pred, color='blue')  # Plot actual values vs predicted values
plt.plot([y.min(), y.max()], [y.min(), y.max()], color='red', linewidth=2)  # Line of equality
plt.xlabel('Actual Values')  # Label for x-axis
plt.ylabel('Predicted Values')  # Label for y-axis
plt.title('Actual vs Predicted Values (Ridge Regression)')  # Title of the plot
plt.grid()  # Add grid for better readability
plt.show()  # Display the plot

Lasso Regression

Lasso regression, also known as L1 regularization, is a technique used in linear regression models. It shares similarities with ridge regression but has distinct features. By applying Lasso regression, we can improve a model’s generalizability through a penalty term that discourages complexity. This approach is summarized by the following formula:

Cost Function: Minimize ||Y−Xθ||**2 + λ*||θ||

Assumptions

In addition to the OLS assumptions Lasso assumes below:

Multicollinearity:

Lasso can handle multicollinearity more effectively than OLS because it includes a penalty term that can shrink coefficients of correlated predictors. This makes it suitable for high-dimensional data.

Sparsity:

Lasso inherently assumes that many of the coefficients are zero, promoting sparsity in the model. This is a key difference from OLS, which does not assume sparsity.

Details

Regularization in LASSO Regression

Penalty Term:
Defined as:

L1=λ×(∣β1∣+∣β2∣+…+∣βp∣)

This term imposes a cost for larger coefficients.

2. Regularization Parameter (λ):
Controls the strength of the penalty: Higher λλ: Increases penalty, shrinking more coefficients to zero and simplifying the model; Lower λλ: Reduces penalty, allowing more flexibility but risking overfitting.

3. Coefficients (β1, β2,…, βp):
Represent the influence of each predictor on the response. LASSO can set some coefficients to zero, effectively performing variable selection.

4. Cost Function:
Combines the residual sum of squares with the L1 penalty:

J(θ) = ||Y−Xθ||**2 + λ×(|β1|+|β2|+…)

Balances data fit and model complexity.

# Import necessary libraries
import numpy as np                  # For numerical operations
import pandas as pd                 # For data manipulation
import matplotlib.pyplot as plt     # For plotting
from sklearn.model_selection import train_test_split  # For splitting the dataset
from sklearn.linear_model import Lasso          # For lasso regression
from sklearn.metrics import mean_squared_error, r2_score  # For evaluating the model

# Step 1: Generate dummy data
np.random.seed(42)  # Set seed for reproducibility

# Create 10 predictor variables
X1 = np.arange(100)
X2 = np.random.rand(100) * 0.1  
X3 = np.random.rand(100) * 0.2 + 0.5 
X4 = 0.5 * X1 - 0.5 * X3 + np.random.rand(100) * 0.1  # X4 is correlated with X1 and X3
X5 = np.random.rand(100)
X6 = -X2 + np.random.rand(100) * 0.1  # X6 is correlated with X2
X7 = np.random.rand(100)
X8 = 3 * X7 + np.random.rand(100) * 0.1  # X8 is correlated with X7
X9 = np.random.rand(100)
X10 = 0.3 * X3 + 0.7 * X4 + np.random.rand(100) * 0.1  # X10 is correlated with X3 and X4

# Combine into a DataFrame
X = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3, 'X4': X4,
                  'X5': X5, 'X6': X6, 'X7': X7, 'X8': X8,
                  'X9': X9, 'X10': X10})

# Step 2: Define the response variable using all predictors
# Here, we use all predictors to define the response variable
y = (3 + 
     2 * X1 - 
     1 * X2 + 
     0.5 * X3 + 
     0.1 * X4 + 
     0.2 * X5 + 
     0.3 * X6 + 
     0.4 * X7 + 
     0.5 * X8 + 
     0.6 * X9 + 
     0.7 * X10 + 
     np.random.rand(100) * 0.5)  # Response variable with noise

# Step 3: Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Step 4: Fit Lasso Regression Model
alpha_value = 1.0  # Regularization strength
lasso_model = Lasso(alpha=alpha_value)

# Fit the model to the training data
lasso_model.fit(X_train, y_train)

# Step 5: Make Predictions
y_pred = lasso_model.predict(X_test)  # Predict on the test set

# Step 6: Evaluate the Model
mse = mean_squared_error(y_test, y_pred)  # Calculate Mean Squared Error
r2 = r2_score(y_test, y_pred)  # Calculate R^2 score

# Output evaluation metrics
print("Mean Squared Error:", mse)  # Print MSE
print("R^2 Score:", r2)  # Print R^2 score

# Step 7: Visualize the Actual vs. Predicted Values
plt.scatter(y_test, y_pred, color='blue')  # Plot actual values vs predicted values
plt.plot([y.min(), y.max()], [y.min(), y.max()], color='red', linewidth=2)  # Line of equality
plt.xlabel('Actual Values')  # Label for x-axis
plt.ylabel('Predicted Values')  # Label for y-axis
plt.title('Actual vs Predicted Values (Lasso Regression)')  # Title of the plot
plt.grid()  # Add grid for better readability
plt.show()  # Display the plot

# Step 8: Display Coefficients
print("Coefficients:", lasso_model.coef_)  # Print the coefficients

Future Work & Conclusion

This article is just scraching the surface of some of the regression techniques. While many more exist — it would also be worthwhile to look into nuances of each technique in while implementing in real life problems. We will look delve deeper into each topic in upcoming artciles. Please comment on which one I should start with.

If you liked the explanation , follow me for more! Feel free to leave your comments if you have any queries or suggestions.

You can also check out other articles written around data science, computing on medium. If you like my work and want to contribute to my journey, you cal always buy me a coffee :)